EJERCICIOS TEMA 12: GEOMETRÍA ESPACIAL
1. ¿De los once cuerpos geométricos, cuáles son poliedros convexos y cuáles son cuerpos de revolución?

a)Poliedro convexo
b)Poliedro convexo
c)Poliedro convexo
d)Poliedro convexo
e)Poliedro convexo
f) Cuerpo de revolución
g)Cuerpo De Revolución
g)Cuerpo De Revolución
h)Poliedro Convexo
i)Cuerpo De Revolución
j)Cuerpo De Revolución
j)Cuerpo De Revolución
k)Cuerpo De Revolución
2. Escribe una tabla para comprobar que la fórmula de Euler se verifica en diferentes poliedros convexos.
Caras (C)
|
Aristas (A)
|
Vértices (V)
|
C+V = A+2
| |
Prisma Rectangular
|
4 caras
|
12 aristas
|
8 vértices
|
4+8= 12+2
|
Prisma Pentagonal
|
5 caras
|
15 aristas
|
10 vértices
|
5+10=15+2
|
Antiprisma Cuadrado
|
10 caras
|
16 aristas
|
8 vértices
|
10+8=16+2
|
Antiprisma Pentagonal
|
12 caras
|
20 aristas
|
10 vértices
|
12+10=20+2
|
Pirámide Triangular
|
4 caras
|
6 aristas
|
4 vértices
|
4+4=6+2
|
Pirámide Triangular Truncada
|
5 caras
|
9 aristas
|
6 vértices
|
5+6=9+2
|
3. Investiga sobre la obra y vida de Arquimedes
Vivió entre (287-212 a.C.)
Se le considera padre de la ciencia mecánica y el científico y matemático más importante de la edad antigua.En el campo de las Matemáticas puras su obra más importante fue el descubrimiento de la relación entre la superficie y el volumen de una esfera y el cilindro que la circunscribe; por esta razón mandó Arquímedes que sobre su tumba figurase una esfera inscrita en un cilindro.
A él le debemos inventos como la rueda dentada y la polea para subir pesos sin esfuerzo. También a él se le ocurrió usar grandes espejos para incendiar a distancia los barcos enemigos.
En Geometría sus escritos más importantes fueron:
- De la Esfera y el Cilindro, donde introduce el concepto de concavidad,así como ciertos postulados referentes a la línea recta.
- De los Conoides y Esferoides en donde define las figuras engendradas por la rotación de distintas secciones planas de un cono.
- De las Espirales en donde analiza estas importantes curvas y analiza sus elementos más representativos.
En Aritmética son, fundamentalmente dos los escritos más interesantes:
- El Arenario en el que expone un método para escribir números muy largos dando a cada cifra un orden diferente según que su posición.
4. Publica en tu blog una entrada con los cinco poliedros regulares también llamados sólidos platónicos. ¿Por qué se llaman así? ¿Y por qué sólo hay 5? ¿De dónde reciben el nombre los sólidos arquimedianos?
Poliedros Regulares :
- Tetraedro
- Cubo
- Octaedro
- Dodecaedro
- Icosaedro
Se denominan así debido a ser sus caras polígonos regulares iguales, y todos sus diedros y ángulos poliedros también iguales.
Un poliedro es regular si todas sus caras son polígonos regulares idénticos y si en todos sus vértices concurren el mismo número de caras. Por lo tanto, es imposible formar un poliedro con solo dos triángulos en cada vértice.
5.
a) ¿Qué figura plana hay que girar y alrededor de que eje para obtener un CILINDRO?
Se obtiene al girar un rectángulo alrededor de un lado.
b) ¿Qué figura plana hay que girar y alrededor de qué eje para obtener un CONO?
Se obtiene al girar un triángulo rectángulo alrededor de un vértice.
c) ¿Qué figura plana hay que girar y alrededor de qué eje para obtener un ESFERA?
Se obtiene al girar un semicírculo desde su centro.
6. Clasifica el siguiente cuerpo geométrico cuyas caras son cuadrados y triángulos equiláteros. ¿Es un poliedro semirregular?
7. ¿Los cuerpos de revolución son convexos?
No, no son convexos, ya que no hay ningún segmento que una dos puntos que esté contenido en dicho cuerpo de revolución.
8. ¿Qué es TRUNCAR un cuerpo geométrico en el espacio? Pon cuatro ejemplos diferentes. ¿Si truncamos un cuerpo geométrico convexo se obtiene siempre otro cuerpo geométrico convexo (o mejor dicho, dos, por cada truncamiento)?
¿Que significa?
Solo existen 5 poliedros regulares, pero existen más polígonos convexos que no son regulares, como es, por ejemplo, la pirámide.
6. Clasifica el siguiente cuerpo geométrico cuyas caras son cuadrados y triángulos equiláteros. ¿Es un poliedro semirregular?
No, no es un poliedro semirregular. Es un sólido, el cual está formado por la suma entre un cubo y una pirámide cuadrangular regular que tiene los aristas de base coincidentes con los aristas de una cara del cubo.
7. ¿Los cuerpos de revolución son convexos?
No, no son convexos, ya que no hay ningún segmento que una dos puntos que esté contenido en dicho cuerpo de revolución.
8. ¿Qué es TRUNCAR un cuerpo geométrico en el espacio? Pon cuatro ejemplos diferentes. ¿Si truncamos un cuerpo geométrico convexo se obtiene siempre otro cuerpo geométrico convexo (o mejor dicho, dos, por cada truncamiento)?
¿Que significa?
significa cortar los vértices o los aristas de dicho cuerpo geométrico.
Ejemplos:
1.Pirámide truncada :
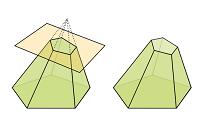
1.Pirámide truncada :

2. Cubo truncado :

3. Tetraedro truncado :

4. Cono truncado :

No siempre, porque hay casos en los que se deshace el hecho de que sea un cuerpo geométrico al diseccionarlo o cortarlo dicho cuerpo,

3. Tetraedro truncado :

4. Cono truncado :

No siempre, porque hay casos en los que se deshace el hecho de que sea un cuerpo geométrico al diseccionarlo o cortarlo dicho cuerpo,
- Se te podría ocurrir hacer la siguiente pregunta: ¿Hay más poliedros convexos?
Solo existen 5 poliedros regulares, pero existen más polígonos convexos que no son regulares, como es, por ejemplo, la pirámide.

No hay comentarios:
Publicar un comentario